Understanding Declination and Convergence

Declination. Caves are usually surveyed with a magnetic compass. Magnetic compasses don't point at the true North Pole. They point at the magnet North Pole. Today, the magnetic North Pole is about 250 miles south of the North Pole. That means that a compass reading will be offset from True North. The amount of the offset varies according the place on the Earth where the reading was taken. This offset is called "Declination."

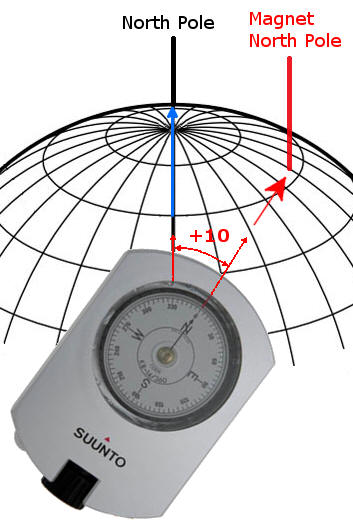
The image to the right illustrates how declination works. In this example, the Magnet North Pole is 10 degrees to the right of the True North Pole. If the compass is aimed right at the Magnetic North Pole, the compass will read zero. However, since the declination is 10 degrees, the compass is really pointing 10 degrees to the right of the North Pole. That makes the real azimuth 10 degrees. From this we can work out the mathematics for handling declination. You simply add the declination to the compass reading to get the vlaue relative to True North. Here's the equation: TN = CR + Declination. TN = True North Reading CR = Compass Reading. As another example, if the compass reading was 25 degrees and the declination was 5, then the actual bearing is 30 degrees relative to True North. 30 = 25 + 5

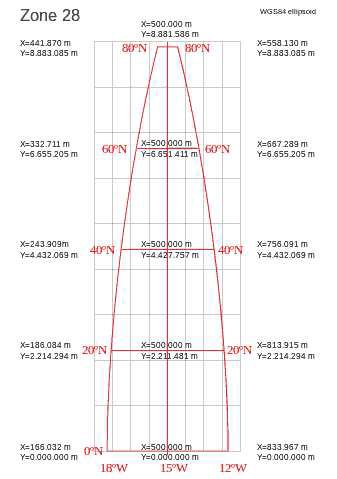
UTM Convergence. UTM coordinates work by mapping a square grid on the surface of the globe. Because of the fact that the globe is a curved surface, the lines of Longitude curve toward the edges of the UTM zone. The image to the right shows a typical UTM zone. The Grid lines are in gray and Longitude lines are in red. The line down the center is called the "Central Meridian and it does not curve.  However, the further you move away from the Central Merian, the more the lines curve. As you can see from the drawing, the lines curve in such a way that they converge at the North Pole. This is where the word "Convergence" comes from. Convergence is the measure of the angle between the red longitude lines and the gray Grid lines. On the east side of the grid, the angle from the Longitude line to the Grid line is positive. Likewise, on the west side the angle is negative. Once you apply declination to a cave survey, the lines in the cave are aligned to True North. If you plot the cave survey on a map that uses UTM, the cave will not be aligned to the UTM grid and the location of the passages will be out of position relative to features on the map.

To solve this problem, you can apply the UTM Convergence angle to a cave survey. The example to the right shows how this is done. Again, convergence angle is measured from the red Longitude line to the black Grid line. Since the angle is clockwise, the value is positive. In this example, the convergence angle is +10 degrees. If you had a passage whose azimuth measured zero degrees, the passage would be aligned to the left-hand dotted red line. Since the dotted red line is counter clockwise from the black line, its angle is minus 10 degrees relative to the grid line. As a result, you always subtract the convergence angle from the azimuth. The formula is thus: GN = TV - Convergence. GN = Grid North Reading TV = True North Value. As another example, if the True North value was 5 degrees and the convergence was 10 degrees, the Grid North value would be -5 degrees: -5 = 5 - 10

Convergence Conventions. Convergence can be measured in two difference ways. These two methods are called 1) the Gauss-Bomford convention and 2) the Survey convention. Here is a description of each one. 1. Gauss-Bomford Convention. In this convention, the angle of the lines of longitude is subtracted from the grid lines. This means that in the Northern Hemisphere, positions to the East of the Central Meridian have positive convergence angles and positions west of the Meridian have negative angles. Positions in the Southern Hemisphere have the opposite signe. This is the most commonly used method of deriving the Convergence angle. It is the method used in Compass and the Geographic Calculator returns convergence values calculated in this way. 2. Survey Convention. In this convention, the angle of the grid lines is subtracted from the lines of longitude. As a result, the Convergence angle has the opposite sign of the Gauss-Bomford convention. This method is only used in Australia and New Zealand. For more information on these two conventions, check out this document:  http://www.iogp.org/pubs/373-21.pdf