Find Blundered Shot Page. This page displays a list of the best candidates for blundered shots. The program looks for blunders by adjusting, one at a time, every single measurement in the loop. It keeps track of which adjustments do the best job of fixing the error. The 30 best fixes are displayed. Here is a detailed description of each item displayed on the page:
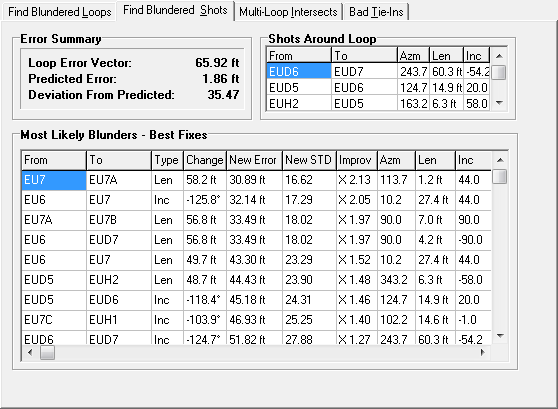
1. Shots Around The Loop. At the top of the screen, the program lists all the shots that form the loop. This allows you go to the Compass Editor and inspect each shot in the loop looking for errors. (Note: the azimuth, length and inclination values are reconstructed from the processed data. The values can be significantly different from the original survey measurements, particularly on the first or last shot in a loop. Also, the shot-order maybe changed by the processing so the azimuth and inclination may be reversed. Finally, if fore- and back-sights are used, the values presented here will be the average of both measurements.)
2. Error Summary. The next section lists the error vector, the predicted error value and the number of standard deviations this error represents.
3. Most Likely Fixes. The bottom section lists the best candidates for blunders. Again, the program looks at every measurement in the loop and does a test adjustment, trying to reduce the final error in the loop. Some of these adjustments will reduce the error a lot and some won’t reduce the error very much. If the test adjustment reduces the error a lot, there is a chance that there is an error in that particular measurement. Thus, the program lists all the adjustments that produced best results. These will be the most likely candidates for blunders. This list displays several items that help you select the best candidates for blunders:
A. From-To. These items shows the "From" and "To" station of the shot that is being tested. Note: the From and To station of a shot may be in the reverse order from the way it was entered in the survey book. This is caused by the way the program processes the data. In other words, the shot A1 to A2 is the same as shot A2 to A1.
B. Measurement. This item indicates which measurement; (azimuth, length or inclination) was adjusted for this shot. This allows you to zero in on both the shot and the exact measurement that maybe causing the problem.
C. Change. Each measurement in the loop is adjusted and, as a consequence, the loop error will be improved by a certain amount. This item shows the amount of change that was applied to this measurement to obtain the improvement. If you were to go back to the raw data and adjust the measurement by this amount, the loop error would improve. The sign (+/-) indicates which direction the change was made. Note: Because of the fact that the program may reverse the shot in order to evaluate it, the sign may be the opposite of what you expect. See item "A" above.
D. New Error Vector. This item shows the size of the loop error after the test adjustment has been made. The error is a composite of the north, east and vertical aspects of the error. The smaller this number is the better the improvement.
E. New Deviation. This item shows the new standard deviation that results from the adjustment. Standard deviation is used because it is the most accurate way of measuring loop quality. If this particular measurement is a blunder, the improvement should result in a new standard deviation that is much better than unadjusted deviation.
F. Improvement. This is the ratio of old error to new error. The larger the improvement ratio, the more likely the measurement is blundered.
G. Azm, Len, and Inc. These are the original Azimuth, Length and Inclination for the shot. These are useful isolating which shots are blundered. For example, let's say the program suggests that a 10-degree inclination adjustment on a shot will close the loop. This means that simply changing the sign on a 5-degree inclination would fix the error. If the shot has a 5-degree inclination, it is a very likely candidate to be blundered.
(Note that since the shot maybe reversed by the processing, the azimuth and inclination may be reversed. Also, if fore- and back-sights are used, the values presented here will be the average of both measurements.)
Example. Blunders show up as very large improvements in the error and standard deviations. The example above is a real survey loop that has 25 shots and is 739 feet long (225m.). I deliberately introduced a ten-foot blunder in the length of shot C10-C9. As you can see, this blunder shows up as 6.1 times improvement in the quality of the loop closure.
You will also notice that other nearby shots show up as likely blunders. This is because they have roughly the same orientation as the actual blunder. Even in situations where you have several good candidates for blunder, you still have narrowed the choices down to a few shots. When you have multiple candidates like this, you can use the Intersect option to help you zero-in on the actual shot. You will also notice that most of the candidates are length measurements. This helps verify that the error is probably a length error.
Station Order. The station-order for shots specified in the blunder list may not match the station order when it was entered in the editor. Internally, the program may need to reverse the order of backsights and other shots in order to analyze them correctly. To maintain external consistency, the program sorts shots into alphabetical order. For example, a backsight may have been entered as A2 -> A1, but because the shot is converted to alphabetical order, it will be listed as A1 -> A2. Also, for the same reason, adjustment values may have the sign value reversed.
Loop Flaws and Math Errors. Occasionally, the program will encounter a survey that makes no sense. For example, having a loop in which all the shot-lengths are zero is an impossible loop. In these situations, the program may have trouble processing the data. For example, it may execute an illegal mathematical operation like divide by zero. If the program encounters a loop with illegal shots, it will display an error message. When you see this error message, it indicates that this particular loop has a bigger problem than just a blunder. It usually indicates things like duplicate shots with different data or two shot loops in which one shot is zero length.
Non-Valid Numbers. The math routines and numeric coprocessor available on most PC’s is capable of handling a non-valid number like infinity. Sometimes the values derived from flawed loops will generate these kinds of numbers. When this happens, the program will display the letters NAN that stands for "Not A Number." For example:
C22 C23 Length 9.08 Ft. 4.13 NAN NAN
When you see NAN values in the blunder detection routines, it indicates severe loop flaws.