|
HOW COMMON ARE BLUNDERS IN CAVE SURVEY DATA?
By Larry Fish
One of the most important problems facing cave surveyors is blunders. Blunders
are fundamental errors in the surveying process and, unlike random errors,
they can have drastic effects on the accuracy of a survey. For this reason,
it would be very useful to know how common blunders are in cave survey data.
Not only does this question have implication about the accuracy of our maps,
but it also has implications for the design of cave survey software.
BACKGROUND: TYPES SURVEY ERRORS
There are three kinds of survey errors: random errors, systematic errors
and blunders. Random errors are generally small errors that occur during
the process of surveying. They result from the fact that it is impossible
to get absolutely perfect measurements each time you read a compass, inclinometer
or tape measure. They are predictable, their effects are generally small
and they can be dealt with using standard statistical techniques.
Systematic errors occur when there is a constant, fixed error being applied
to the data. For example, they could be caused by a bent compass needle,
a stretched tape or a distortion of the earth's magnetic field. In some cases,
they can be corrected by simply subtracting a constant from the data.
Blunders are fundamental errors in the surveying process. Blunders are usually
caused by human error. They are mistakes in the processing of taking, reading,
transcribing or recording survey data. Some typical blunders would be: reading
the wrong end of the compass needle, transposing digits written in the survey
book, or tying a survey into the wrong station. The thing that makes blunders
so important is that they can produce very large and unpredictable errors.
TESTING CAVES FOR BLUNDERS
The COMPASS survey software has a feature that calculates the percentage
of loops in a cave that are blundered. The feature is designed give you an
overall sense of the quality of the surveys in a cave.
The process of finding blunders begins with an estimate of the typical errors
that would be found in surveying instruments. The values are specified as
standard deviations of the instruments. For example, the standard deviation
for a typical survey compass might be 2 degrees.
The program then walks around each loop, projecting the expected errors through
each shot and mathematically combining the result. This gives you a predicted
error level for the whole loop if all the errors are random. Thus, any loop
who's errors exceed the prediction are probably blundered. COMPASS lists
the percentage of loops that exceed two standard deviations from the prediction.
Because of the way the statistics work, any loop error greater than two standard
deviations over the prediction has a 95.4% chance of being blundered.
Over the years, people have sent me a large number of survey files from caves
around the world. I currently have more than 250 data sets from a wide variety
of caves. To determine how common blunders are, I tested the survey data
from a range of representative caves.
The following table illustrates the percentage of blundered loops in 16 caves
from the U.S. and Mexico. I have lots of smaller caver, but I chose caves
that had enough loops to give meaningful results. The chart represents the
percentage of loops in each cave that has at least one blunder. For the test,
I set the predicted instrument standard deviations at two degrees for compass
and inclinometer and 0.1 foot (3 cm.) for the length measurement.
| Cave Name |
Number Loops |
Percent Blund. |
Location |
Length |
|
| Alexander's |
17 |
65% |
? |
2-miles |
3.2-km. |
| Fixin' |
7 |
57% |
Colorado |
1.5-miles |
2.4-km. |
| Groaning |
70 |
49% |
Colorado |
9.1-miles |
14.6-km. |
| Lechuguilla |
1142 |
32% |
New Mexico |
100.5-miles |
160.6-km. |
| Cheve |
36 |
30% |
Mexico |
16-miles |
25.7-km. |
| Blue |
46 |
28% |
Eastern US |
28-miles |
45.0-km. |
| Wind |
900 |
25% |
South Dakota |
71-miles |
114.2-km. |
| St.Augustin |
20 |
25% |
Mexico |
10-miles |
16.0-km. |
| Kazamura |
83 |
19% |
Hawaii |
38.5-miles |
61.9-km. |
| Carlsbad |
813 |
16% |
New Mexico |
22.1-miles |
35.5-km. |
| Lilburn |
238 |
14% |
California |
16.4-miles |
26.3-km. |
| Fulford |
14 |
14% |
Colorado |
1.0-miles |
1.6-km. |
| Cave Of The Winds |
17 |
13% |
Colorado |
2.0-miles |
3.2-km. |
| Fairy |
29 |
12% |
Colorado |
1.5-miles |
2.4-km. |
| Spider |
149 |
11% |
New Mexico |
3.5-miles |
5.6-km. |
| Roppel |
333 |
2% |
Kentucky |
69.1-miles |
111.2-km. |
|
| Average |
230 |
26% |
24.7 |
39.7 |
|
The data here represents a wide variety of caves, survey styles and surveying
eras. For example, Groaning and Fixing are tight, crawly maze caves with
difficult surveying conditions. Their entrances are at about 10,000 feet
(3048 m.) of elevation and the year round temperature is 39 degrees (4 C.).
It is not surprising that the blunder level is high in these caves. Lechuguilla
is a less challenging cave, but the chaos of large expeditions and the rapid
pace of discovery produced lots mis-tie errors. Finally, the Wind Cave data
actually has surveys dating back to 1934.
The majority of the caves were surveyed by cavers from the United States
using U.S. style surveying techniques. It would be interesting to know if
surveyors from other countries, using different techniques would get different
results.
As you see from the chart, there are a surprisingly large number of blundered
loops. In fact the average cave in the list has 60 blunders. In many ways
this is not surprising given the difficult environment and the large number
of measurements that make up a cave survey.
ESTIMATING INSTRUMENT ERRORS
While I was working on this project, Olly Betts suggested an experiment that
might show us something about instrument errors. He suggested that we gradually
increase the projected instrument errors and see what happened to the percentage
of blunders. The result was very interesting.
I started with 0.5 degrees STD for compass and inclinometer and 0.25 foot
for tape. I then tested the percentage of blunders and increased the values
by 0.5 degrees and 0.025 foot for tape. I did this for four caves representing
a range of survey quality. Here is a chart of the result:
| Comp/Inc |
Tape |
Lech |
Wind |
Lilburn |
Roppel |
| STD |
STD |
% Blnd. |
% Blnd. |
% Blnd. |
% Blnd. |
| 0.5 |
0.025-ft. |
79.5 |
75.4 |
68.5 |
68.5 |
| 1.0 |
0.050-ft. |
56.1 |
52.9 |
39.5 |
25.5 |
| 1.5 |
0.075-ft. |
40.5 |
36.4 |
22.3 |
7.5 |
| 2.0 |
0.100-ft. |
32.0 |
25.8 |
14.7 |
2.4 |
| 2.5 |
0.125-ft. |
26.0 |
19.6 |
12.2 |
0.3 |
| 3.0 |
0.150-ft. |
21.2 |
16.1 |
10.5 |
0.0 |
| 3.5 |
0.175-ft. |
17.3 |
13.8 |
9.7 |
0.0 |
| 4.0 |
0.200-ft. |
14.1 |
11.8 |
8.8 |
0.0 |
| 4.5 |
0.225-ft. |
12.6 |
10.2 |
8.8 |
0.0 |
| 5.0 |
0.250-ft. |
11.4 |
9.2 |
8.4 |
0.0 |
| 5.5 |
0.275-ft. |
10.2 |
8.2 |
7.6 |
0.0 |
| 6.0 |
0.300-ft. |
9.2 |
7.7 |
7.6 |
0.0 |
| 6.5 |
0.325-ft. |
8.3 |
7.1 |
7.6 |
0.0 |
| 7.0 |
0.350-ft. |
8.0 |
6.4 |
7.6 |
0.0 |
| 7.5 |
0.375-ft. |
7.4 |
5.9 |
7.6 |
0.0 |
| 8.0 |
0.400-ft. |
7.0 |
5.4 |
7.1 |
0.0 |
| 8.5 |
0.425-ft. |
6.6 |
5.2 |
7.1 |
0.0 |
| 9.0 |
0.450-ft. |
6.4 |
4.9 |
7.1 |
0.0 |
| 9.5 |
0.475-ft. |
6.2 |
4.3 |
7.1 |
0.0 |
| 10.0 |
0.500-ft. |
5.8 |
4.1 |
7.1 |
0.0 |
| 10.5 |
0.525-ft. |
5.7 |
3.9 |
7.1 |
0.0 |
| 11.0 |
0.550-ft. |
5.5 |
3.8 |
7.1 |
0.0 |
| 11.5 |
0.575-ft. |
5.5 |
3.8 |
6.7 |
0.0 |
| 12.0 |
0.600-ft. |
5.1 |
3.6 |
6.7 |
0.0 |
| 12.5 |
0.625-ft. |
4.9 |
3.1 |
6.7 |
0.0 |
| 13.0 |
0.650-ft. |
4.7 |
2.9 |
6.7 |
0.0 |
| 13.5 |
0.675-ft. |
4.6 |
2.9 |
6.3 |
0.0 |
| 14.0 |
0.700-ft. |
4.5 |
2.9 |
6.3 |
0.0 |
| 14.5 |
0.725-ft. |
4.3 |
2.8 |
6.3 |
0.0 |
| 15.0 |
0.750-ft. |
4.1 |
2.8 |
6.3 |
0.0 |
I have also included a graph of the results that is much easier to understand.
As you can see, as the standard deviations for the instruments increase,
the percentage of blundered loops drops rapidly and then flattens dramatically.
The best cave flattens out at about 2.5 degrees of standard deviation and
the lower quality caves around 7 degrees.
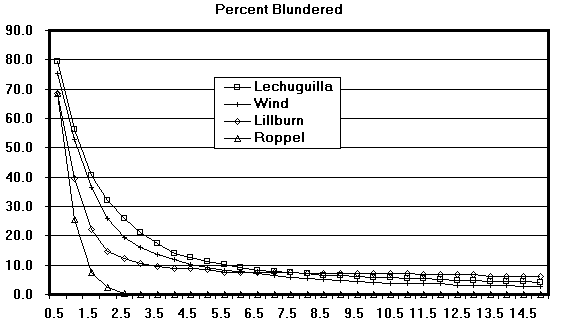
I think it is easy to understand what is happening here. As the standard
deviations increase, large numbers of the better quality loops are eliminated
from the group of blunders and so the percentage goes down rapidly. At some
point, all we have left are loops with severe blunders that have not eliminated
by the higher standard deviations. Clearly, the loops below the inflection
point are blundered. You would never expect to have random errors of 10 or
15 degrees in a compass or inclinometer. Likewise, the loops at the very
top of the curve must be blunder free.
Obviously, the sudden flattening of the curve represents the point at which
we shift from unblundered loops (with high instrument standard deviations)
to blundered loops. Thus, this point represents the maximum standard deviation
for the instruments.
By looking at the graph and calculating the first and second derivatives,
it is easy to estimate the point where each line goes flat. Here is list
of my estimates:
| Lechuguilla - |
7.5 Degrees |
0.375 ft. |
11.4 cm. |
| Wind - |
5.5 Degrees |
0.275 ft. |
8.2 cm. |
| Lillburn - |
5.0 Degrees |
0.250 ft. |
7.6 cm. |
| Roppel - |
3.0 Degrees |
0.150 ft. |
4.5 cm. |
The values may seem surprisingly large, but they are similar to other
experimental values. For example, the March 1998 issue of Compass Points
has an article describing the analysis of compass errors in an outdoor
test-course. In spite of a relatively simple course and the use of experienced
surveyors, some of the compass errors were in the range of 6 degrees.
Measuring instrument error this way has two advantages over the traditional
survey course method of determining instrument errors. First, the values
are based on the combined effects of thousands of measurements, with hundreds
of different instruments, done by hundreds of surveyors, each using different
survey techniques. Second, it enables us to look at the performance of
instruments and surveyors in widely varying survey environments.
One disadvantage of this technique is that it gives you a composite error
value that doesn't tell you anything about the individual instruments. It
could be, for example, that the actual tape errors are much smaller and compass
errors much larger than given here. Perhaps, a more complicated test would
give separate values for the individual instruments.
CONCLUSION. In conclusion, it appears that blunders are a common problem
in cave surveying, particularly for certain classes of caves. Also, examining
real-world data is a very valuable technique for estimating the general quality
of survey data and survey instruments. One advantage of the technique is
that it tests the composite performance many different instruments and many
different surveyors.
|

