Loop Closure
Loops. Many caves have passages that wind around in a circle and connect
back to themselves. When a survey connects back to itself, it called a loop.
If a loop is surveyed perfectly, the survey should come back to the exact
point at which it started. If the loop doesn't come back to the exact starting
point it is called a closure error. Closure errors indicate that some or
all of the survey measurements within a loop have errors.
Closing Loops. If the closure errors are large enough, the shape of
the loop and the shape of the cave will be distorted by the errors. For this
reason, cave survey programs must have a way of dealing with the effects
of these errors. This process of dealing with loop errors is called "closing"
loops. Closing loops is a mathematical process that systematically spreads
the errors around the cave to minimize the effect of the error on any one
shot. In effect, it gives you lots of little errors instead of one big error
at the point where the loops close. In this way, there is only minimal distortion
of the passages.
Error Types. The kind of error found in a loop has a big effect on
how the loops can be closed. There are three types of error in survey data:
random errors, systematic errors and
blunders.
-
Random Errors. Random errors are generally small errors that occur
during the process of surveying. They result from the fact that it is impossible
to get absolutely perfect measurements each time you read a compass, inclinometer
or tape measure. For example, your hand may shake as you read the compass,
the air temperature may affect the length of the tape, and you may not aim
the inclinometer precisely at the target.
-
Systematic Errors. Systematic errors occur when something causes a
constant and consistent error throughout the survey. Some examples of systematic
error are: the tape has stretched and is 2 cm too long, the compass has five
degree clockwise bias, or the surveyor read percent grade instead of degrees
from the inclinometer. The key to systematic errors is that they are constant
and consistent. If you understand what has caused the systematic error, you
can remove it from each shot with simple math. For example, if the compass
has a five degree clockwise bias, you simply subtract five degrees from each
azimuth.
-
Blunders. Blunders are fundamental errors in surveying process. Blunders
are usually caused by human errors. Blunders are mistakes in the processing
of taking, reading, transcribing or recording survey data. Some typical blunders
are: reading the wrong end of the compass needle, transposing digits written
in the survey book, or tying a survey into the wrong station.
Least Squares. Most programs use a process for closing loops called
Minimizing Least Squares. Least Squares works by solving
a large equation that take into account all the redundant data and minimizes
the errors. Least Squares assumes that the errors in the survey
are random. If the errors are not random, the data violates the mathematical
model of Least Squares and the process will not work properly.
As a result, if you are going to use Least Squares, special
steps must be taken to detect any blunders and compensate for them.
Unfortunately, most cave survey programs that use Least Squares
do not take the extra steps necessary to deal with blunders. In fact, at
this time (March, 2001) the only program I'm aware of that correctly
implements Least Squares, is Survex a British surveying
program.
Handling Blunders. If a program uses Least Squares and
does not handle blunders, the effect is spread the blunder error throughout
the cave. This causes well surveyed loops to be contaminated by the errors
in the badly surveyed loops. If blunders weren't very common in cave surveys,
this might not be a problem, but blunders are very common. I looked at 16
large and relatively famous caves like, Wind, Lechuguilla, Lillburn and
Lechuguilla and, on avergage, 26% of the loop had blunders in them. During
a recent resurvey of Cave of the Winds, Paul Burger found, on average, one
blunder for every 20 shots surveys. Here are some links to more information
on loop closure:
Loop Closure In COMPASS. COMPASS uses a loop closure technique
that was used by surveyors and cartographers before modern computer were
available. It works by closing the best loops first and locking them down
so they cannot change. Thus, the worst loops are closed last and the errors
from the worst loops are confined to that part of the cave. This way the
errors from worst loops cannot spread to contaminate the good loops. This
gives a result that is very similiar to a properly done Least Squares, but
it is much faster.
The COMPASS loop closer also writes the closed data to a file that
is identical to the raw survey data, except that the shot data has been adjusted
to close the loops. This means that you can actually test the data and see
that the loop errors have gone to zero. You can also look at which shots
the closer adjusted. This is useful for finding blunders.
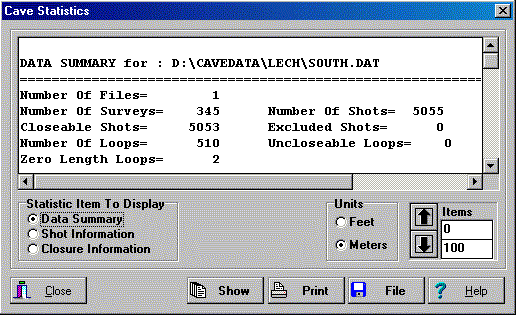
This screen shows general information about the loop closure process. Here,
the display shows that there are two loops where length of the loop is zero.
Zero length loops cannot be closed and they may indicate a data entery error.
Also, some loops cannot be closed because all the shots in the loop have
excluded from closing.
Station Information:
Index Station Parent Len Azm Dip Status
===========================================================================
100 - FE19 99 38.7m. 110.3 6.0 UnClosed ($0000)
101 - FE20 100 38.1m. 95.8 20.0 UnClosed ($0000)
102 - FE21 101 43.3m. 150.4 -2.0 UnClosed ($0000)
103 - FE22 102 52.2m. 260.9 -28.0 UnClosed ($0000)
104 - FE23 84 68.7m. 168.3 -18.6 Closed ($0001)
|
The statistics display also shows how each shot was handled and the resulting
adjustment. Here the statistics show four unclosed shots and one closed shot.
The unclosed shots may not be part of a loop or they may be specifically
excluded from closing.
Closure Information:
===================================================================
Index: 50 Station One: 981 Station Two: 907 Common: 907
Loop Length: 402.8m.
Residual Error - North: 0.0000m. East: 0.0000m. Vert.: 0.0000m.
Loop Status: Closed ($0001)
Closure Is Between: FFP4-FFN29
FFP4,FFN92,FFN91,FFN90,FFN89,FFN29
Common point: FFN29
FFN29
--------------------------------------------------------------------
Index: 51 Station One: 983 Station Two: 903 Common: 903
Loop Length: 619.7m.
Residual Error - North: 0.0000m. East: 0.0000m. Vert.: 0.0000m.
Loop Status: Closed ($0001)
Closure Is Between: FFP6-FFN25
FFP6,FFP5,FFN29,FFN28,FFN27,FFN25
Common point: FFN25
FFN25
|
The final statistical display shows how the each loop has been effected by
closure process. Here you see two loops whose residual errors are zero. If
for some reason, the program wasn't able to close one of the loops, the errors
would not be zero.
|

